Super User
MÉTODOS MULTI-ESCALA PARA A SIMULAÇÃO NUMÉRICA DE RESERVATÓRIOS DE PETRÓLEO
Professor: Luis Felipe Feres Pereira
9.2.1 Resumo:
Os reservatórios de petróleo localizados no pré-sal brasileiro são bastante profundos (podendo chegar a 1 Km de profundidade), em contraste com reservatórios usuais que possuem apenas alguns metros na direção vertical. A simulação numérica eficiente (rápida e precisa) de escoamentos multifásicos nos reservatórios grandes do pré-sal apresenta novos desafios (ligados aos problemas computacionais de grande porte) que não são resolvidos adequadamente por simuladores comerciais disponíveis no mercado. Estes simuladores, que foram desenvolvidos com o objetivo de realizar simulações numéricas de reservatórios consideravelmente menores do que os encontrados no pré-sal, são muito lentos quando utilizados em reservatórios de interesse para a indústria do petróleo brasileira. Simuladores devem fazer uso de métodos numéricos inovadores, capazes de tirar proveito de arquiteturas de última geração do tipo multicore, na simulação eficiente de problemas de recuperação de petróleo de grande porte.
Métodos numéricos multi-escala para problemas elípticos e parabólicos possuem potencial para tirar proveito de tais arquiteturas, pois problemas grandes são decompostos em diversos problemas menores que podem ser resolvidos em cores distintos. O desenvolvimento de simuladores para a indústria de petróleo que fazem uso de técnicas multi-escala é um tópico que tem atraído a atenção de diversos grupos de pesquisa. Mencionamos, por exemplo, os trabalhos recentes de [2,3]. No entanto, cabe ressaltar que nestes dois trabalhos os algoritmos não foram desenhados para processamento em paralelo.
O problema modelo para o desenvolvimento de técnicas multi-escala é a equação para pressão em escoamentos monofásicos em meios porosos. Sugerimos ao leitor a publicação [4] para referencias e também para uma comparação de vários procedimentos deste tipo desenvolvidos até 2008. Estes métodos utilizavam condições de fronteiras ad-hoc na construção de funções de base multi-escala. Desenvolvimentos mais recentes incluem [1,5,6,7], nos quais procedimentos mais precisos tem sido investigados. O grupo de pesquisa ligado ao Prof. Pereira fez uso de técnicas de decomposição de domínios no desenvolvimento do método MuMM (Multiscale Mixed Method, veja [1]) evitando assim o uso de condições de fronteira que geram imprecisões no cálculo da velocidade. No trabalho apresentado em [1] um algoritmo iterativo para a decomposição de domínios é definido, tirando proveito de malhas múltiplas e uma nova família de funções de base multi-escala. As novas funções de base são definidas para representar soluções discretas em subdomínios. Este procedimento apresenta algumas propriedades que devem ser ressaltadas:
A aproximação é localmente conservativa por conta da utilização de elementos finitos mistos. Coeficientes descontínuos (situação típica encontrada na simulação de reservatórios de petróleo) e termos de fonte podem ser considerados.
Três escalas de comprimento são introduzidas na definição do procedimento: a solução é procurada na escala mais fina; funções de base multi-escala são definidas nos subdomínios associados à maior das três escalas. A conservação do fluxo, indispensável para no estudo de escoamentos em meios porosos, é diretamente imposta em uma escala intermediária.
Se a maior e a menor escala coincidem então o novo método reproduz exatamente a solução por elementos finitos mistos na escala mais refinada.
O esquema iterativo entre subdomínios, que é baseado nas condições de interface de Robin impostas na escala intermediária, é de implementação simples.
O procedimento se adequa bem a unidades de processamento heterogêneas (CPU-GPU): todos os problemas locais podem ser eficientemente resolvidos em GPUs.
Os objetivos deste mini-curso são: (i) Apresentar uma introdução à modelagem de escoamentos multifásicos em meios porosos e (ii) Desenvolver software paralelo para o método multiescala MuMM, que se baseia em uma técnica de decomposição de domínio de [2].
9.2.2 Pré-requisitos:
Experiência com uma das seguintes linguagens de programação: C, C++ ou Fortran. Por exemplo, no caso da linguagem C, os alunos devem ter familiaridade com os primeiros 5 capítulos de [9]. Uma observação: Se você tem bons conhecimentos de MATLAB e deseja fazer este curso, com três ou quatro dias de trabalho você tem condições de entender o material citado do livro [9].
9.2.3 Ementa:
Os seguintes tópicos serão discutidos neste mini-curso:
1. Introdução a escoamentos em reservatórios de petróleo: escoamentos monofásicos e bifasicos
2. A pressão global para problemas bifásicos; Quebra de operadores
3. O problema elíptico
4. Discretização por elementos finitos mistos
5. O método de [8]
6. O método de [1]
7. Introdução a MPI, “messagepassing interface” (http://mpitutorial.com/tutorials/)
8. Desenvolvimento de códigos para processamento serial e em paralel
9.2.4 Programa para as aulas:
Aula #1: Serão discutidos os tópicos 1-6 da ementa.
Aula #2: Desenvolvimento de software para processamento serial.
Aulas #3-5: Tópico 7 da ementa. Desenvolvimento de software para processamento em paralelo.
Aula #6: Conclusão dos projetos e competição final. Serão outorgados prêmios para os dois códigos paralelos mais rápidos desenvolvidos no curso.
9.2.5 Arquivos:
9.2.6 Referências:
[1] A. Francisco, V. Ginting, F. Pereira, J. Rigelo, Design and Implementation of a Multiscale Mixed Method for Porous Media Flows, Mathematics and Computers in Simulation, 99, (2014) 125-138.
[2] H. Hajibeygi, H. Tchelepi, Compositional Mutiscale Finite-Volume Formulation SPE-163664-PA, SPE Journal, 2014.
[3] A. Kozlova, J. R. Natvig, S. Watanabe, Y. Zhou, K. Bratvedt, S. H. Lee, A Real-Field Multiscale Black-Oil Reservoir Simulator, SPE-173226-MS, 2015.
[4] V. Kippe, J. E. Aarnes and K. Lie, A comparison of multiscale methods for elliptic problems in porous media flows, Computational Geosciences, Vol. 12, Number 3, (2008) 377-398.
[5] Y. Efendiev, T. Hou, Multiscale finite element methods: theory and applications. Springer, (2009).
[6] M. Wheeler, T. Wildey and G. Xue, Efficient algorithms for multiscale modeling in porous media flows, Numer. Linear Algebra Appl., 17, (2010) 771-785.
[7] B. Ganis and I. Yotov, Implementation of a mortar mixed finite element method using a multiscale flux basis, Computer Methods in Applied Mechanics and Engineering, 198 (2009) 3989-3998.
[8] J. Douglas, Jr., P. J. PaesLeme, J. E. Roberts, and J. Wang, A parallel iterative procedure applicable to the approximate solution of second order partial differential equations by mixed finite element methods, Numer. Math., 65 (1993) 95--108.
[9] B. Kernighan and D. Richtie, The C Programming Language, 2nd Edition, Prentice Hall Software Series.
SCALING LIMITS OF MARKOV PROCESSES AND APPLICATIONS TO COMMUNICATION SYSTEMS
Matthieu Jonckheere
The constant technological evolution and developments in the area of telecommunication lead to challenging research questions regarding performance evaluation and design of actual and future communication systems. Stochastic networks are mathematical models describing a wide variety of high dimensional complex systems, seemingly of very different nature, from telecommunication and information systems to manufacturing environments. An in-depth understanding of their dynamics is of critical importance for many applications, e.g., the dimensioning and implementing efficient control schemes for a wide range of wireless networks. In particular, characterizing the stability region (set of parameters where the network can function properly) of large networks is both a complex theoretical problem and the most crucial benchmark of performance analysis.
However, the scale of the order of components of these systems often makes low-dimensional tools of classical queuing theory useless to obtain appropriate performance evaluation tools and design efficient algorithms. On the contrary, scaling methods that have a lot in common with mechanical statistics, particle systems or large random graphs might be of great help to deal with such high-dimensionality.
In each case, the effect of local interactions are studied at a macroscopic scale, raising drastically different behaviors depending on a small number of macroscopic parameters like temperature and pressure, which can be translated for communication and information networks in terms of probability of transmissions and density of users. Another important component of many communication systems is the random locations of the components. An interesting line of research combines stochastic geometry and scaling techniques.
We provide here an introduction to various scaling techniques intervening in the analysis of stochastic networks and random graphs, allowing to connect the analysis and optimisation of very complex stochastic systems to simpler ones (deterministic dynamical systems or diffusions).
The course is designed to interact directly with the participants. Three sessions of lectures are scheduled (about 12 hours). The rest of the time will be reserved to solve networking problems by supporting and coaching the participants.
9.1.1 Scheduling:
Lecture 1 – An introduction to Markov processes and their scaling limits via martingales.
One dimensional examples: MM1 and MMinfinity.(4 hours).
Homework: some matlab examples of functional law of large numbers and diffusions approximations of MM1 and MMinfinity.
Lecture 2 – Multidimensional examples. Jackson networks.
Averaging principles. Connections with stability analysis.
Presentation of the problem of optimizing the transmission of a downlink wireless base station. Asymptotically optimal policies. (4 hours)
Home work: Code a two-dimensional example.
Lecture 3. Mean-field scaling limits. Principle and examples.
Presentation of a last example on communication on random graphs. (3 hours)
Home work: simulation of random graphs and exploration processes.
Lecture 4: questions and answers on the examples considered.(3 hours)
Languages: Presentations and coaching activities will be in english.
9.1.2 Bibliography
1) Markov Chains: Gibbs Fields, Monte Carlo Simulation, and Queues, P. Brémaud Springer
2) Convergence of Markov processes, notes, M. Hairer,
3) Markov chains and stochastic stability, S. Meyn and R. Tweedie,
4) Cambridge Stochastic networks and queues, Ph. Robert Springer
Histórico e Objetivos
A qualidade da pesquisa em Ciências Matemáticas (CM) no Brasil é considerada de muito bom nível, como atestam a recente concessão de uma medalha Fields para um brasileiro ou a classificação do Brasil como nível IV na IMU (International Mathematical Union). No entanto, essa pesquisa tem cunho quase que exclusivamente acadêmico. Várias experiências em países desenvolvidos atestam que as Ciências Matemáticas podem contribuir de maneira decisiva para a inovação, geração de novos conhecimentos e tecnologias e agregar valor a produtos e processos (Relatório Deloitte sobre o Benefício Econômico da Pesquisa em Matemática na Inglaterra).
No CEPID-CeMEAI nos propusemos a modificar essa realidade promovendo contacto com problemas industriais por meio dos workshops com a indústria que realizamos periodicamente. É bastante comum em outros centros, por exemplo, no OCIAM em Oxford, realizar-se uma Escola de modelagem na semana anterior ao Workshop para proporcionar aos alunos de Pós-graduação, como treinamento para o evento da semana posterior. Nessa Escola são apresentados problemas reais já estudados em ocasiões anteriores para os quais se tem uma boa base de conhecimento e os alunos trabalham durante uma semana, guiados pelo tutor na solução ou estudo desses problemas. Com isso espera-se que esses alunos estejam mais bem preparados para o workshop a seguir e possam contribuir de maneira efetiva para a solução dos problemas reais a serem trabalhados. (Outros Study Groups with Industry no mundo)
III WSMPI - 3rd Brazilian SGI (2016)
3º Workshop de Soluções Matemáticas para Problemas Industriais (3rd Brazilian Study Group with Industry)
http://www.cemeai.icmc.usp.br/3WSMPI/
Problemas
1) Divergent Beam Transform from a ∂-equation [pdf]
Empresa - LNLS
2) Controle de endo e ectoparasitos em bovinos de corte por meio da análise da infectividade [pdf]
Empresa - UFMG
3) Tyre Burst Numerical Simulation [pdf]
Empresa - Embraer
4) Score único [pdf]
Empresa - BoaVista SCPC
5) Traffic prediction algorithm via data analysis [pdf]
Empresa - Splice
6) Testing environments & optimization [pdf]
Empresa - AMDOCS
Estressômetro
Notícias Relacionadas
Pesquisadores
Jó Ueyama, Gabriel Giancristofaro, Eduardo Vasconcelos, José Torres Neto e Leandro Mano“Você pode estar nervoso, com sono ou cansado. Não acha melhor parar o veículo no próximo posto?”. Este poderia ser um alerta enviado a um motorista, caso o estressômetro estivesse operando em algum dispositivo próximo a ele.
Coordenada pelo pesquisador Jó Ueyama, da área de Inteligência Computacional do Centro de Ciências Matemáticas Aplicadas à Indústria (CEPID-CeMEAI), com colaboração dos alunos Gabriel Giancristofaro, Eduardo Vasconcelos, José Torres Neto e Leandro Mano, do Instituto de Ciências Matemáticas e de Computação (ICMC/USP), a tecnologia se baseia no desenvolvimento de um software que combina ferramentas comuns de dispositivos eletrônicos – reconhecimento da tonalidade da voz, câmera, sensores de movimento e de luminosidade – para monitorar o humor dos usuários, podendo detectar estresse elevado, sinais de depressão ou outros tipos de emoções.
Aplicações para beacons
Notícias Relacionadas
Pesquisadores
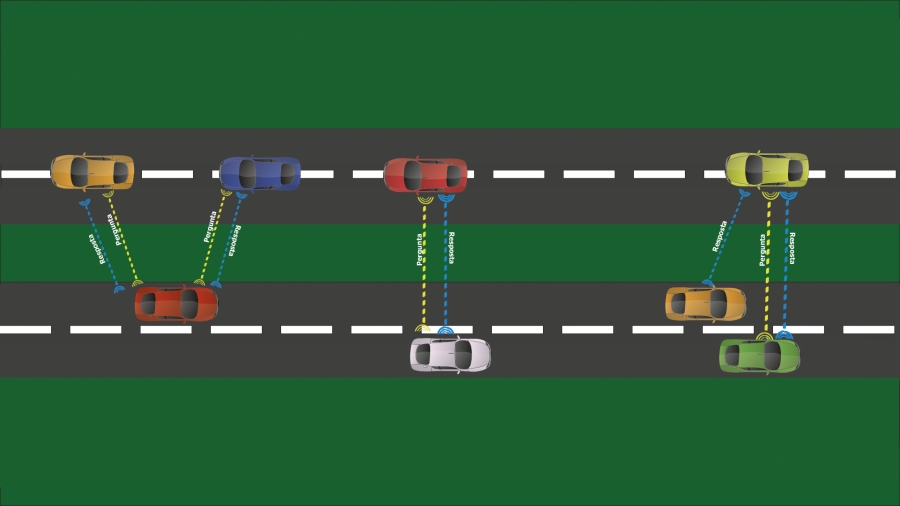
Edson MoreiraAinda não é comum nas ruas ou estradas, mas a comunicação entre carros e entre os carros e a infraestrutura viária não demora a chegar. Muitas montadoras já tem lançado a tecnologia V2V - Vehicle to Vehicle - na fabricação de alguns automóveis.
Um recurso de emissão de sinais de rádio, semelhantes ao wi-fi, que poderá propiciar a troca de informações entre carros e com a infraestrutura da estrada. E que poderá propiciar ainda modelos novos de negócios envolvendo a geração de serviços e propagandas nas estradas. Este é o principal foco de uma pesquisa coordenada pelo professor Edson Moreira e que tem apoio da FAPESP - por intermédio do CEPID-CeMEAI.
Túneis de vento
Notícias Relacionadas
Pesquisadores
Maria Luisa Reis, João Luiz AzevedoQuando um veículo está em movimento, seja ele um carro, um navio, um avião ou até um VANT, ele é submetido à ação do vento. Prédios, casas ou qualquer outra construção também recebem essa força e precisam ser capazes de suportá-la para que não haja danos na estrutura.
Imagine que um modelo de avião terá uma pequena mudança em sua aerodinâmica, mas a melhor configuração dessa mudança ainda não é conhecida. É necessário realizar alguns testes, mas é inviável construir um avião diferente para cada uma das tentativas – além de muito caro, é extremamente perigoso. Então, como é possível testar as mudanças – ou até novos modelos – sem colocar a aeronave no ar?
No Departamento de Ciência e Tecnologia Aeroespacial (DCTA), em São José dos Campos, pesquisadores do Instituto de Aeronáutica e Espaço (IAE) contam com três túneis de vento, equipamentos que servem exatamente para simular o deslocamento do ar, chamado de escoamento, em estruturas.
Estudo do atrito entre as peças nos motores de carros
Notícias Relacionadas
Pesquisadores
Gustavo Buscaglia, Hugo Checo SilvaA pesquisa focou-se no desenvolvimento de métodos numéricos para a simulação de contatos lubrificados, normalmente encontrados nos motores de carros, por exemplo. Um contato lubrificado são duas superfícies em movimento relativo, com a separação entre elas sendo preenchida por um fluido, o lubrificante.
Uma ou ambas dessas superfícies são fabricadas seguindo algum procedimento mecânico ou mais recentemente outros métodos - laser, por exemplo. Essas superfícies têm detalhes da ordem dos micrômetros. O objetivo do estudo foi analisar o desempenho do dispositivo lubrificado em termos de força de atrito, desgaste e potência perdida para diversas dessas micro-superfícies.
A pesquisa foi desenvolvida em parceria com pesquisadores do Institut National des Sciences Appliquées de Lyon (França). Do lado da indústria, tivemos parcerias com a Renault da França e com o departamento de pesquisa no Brasil da Mahle, um fabricante de peças de carro que tem base em Stuttgart, Alemanha.
MODELAGEM ESTOCÁSTICA E QUANTIFICAÇÃO DE INCERTEZAS
Rubens Sampaio
Trata-se de um curso de uma semana. Uma parte das aulas serão teóricas, e outras de exercícios. Os alunos tomaram parte ativa fazendo exercicios e apresentações de alguns artigos escolhidos. Dois livros de Notas de Matematica Aplicada da SBMAC serão usados como texto.
1. Motivação. Conceito de evento e probabilidade. Independência. Exemplos.
2. Espaço de probabilidades. Probabilidade discreta e enumerável. Regras de contagem. Caminhos aleatórios.
3. Variáveis aleatórias inteiras. Esperança. Momentos. Variáveis aleatórias reais. Processos estocásticos.
4. Probabilidade Condicional. Convergência de sequências de variáveis aleatórias. Desigualdades.
5. Geração de variáveis aleatórias e método de Monte Carlo. Simulações com Matlab.
6. Estatísticas e distribuição normal. Teorema do limite central. Lei dos grandes números.
7. Processos de Poisson. Confiabilidade.
8. Entropia e Informação. Princípio do máximo de entropia.
9. Cadeias de Markov. MCMC
9.4.1 Referências
[1] Geoffrey Grimmett and DominicWelsh Probability: an introduction Claredon Press, Oxford, 1986.
[2] José Eduardo Souza de Cursi e Rubens Sampaio Modelagem Estocástica e Quantificação de Incertezas Notas de Matematica Aplicada da SBMAC, volume 66
[3] R. Sampaio e R. Lima Modelagem estocástica e geração de amostras de variáveis e vetores aleatórios Notas em Matemática Aplicada da SBMAC, volume 70